half life formula pharmacology
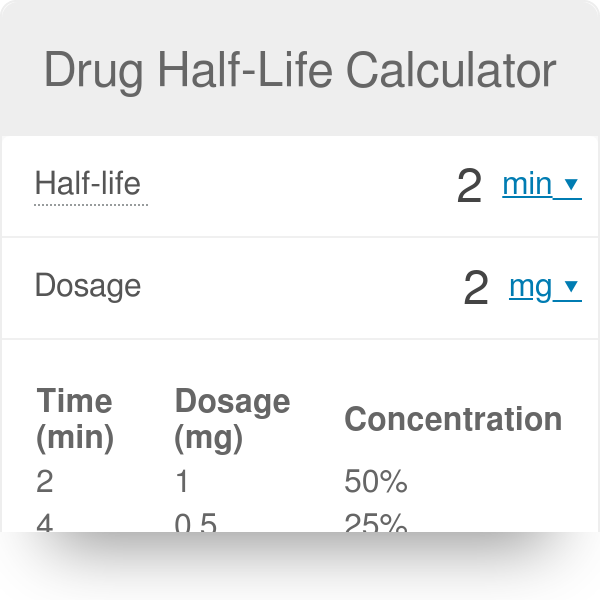
After 1 half-life 50 of the drug is gone. After 4 5.
For more tutorials see our pharm playlist at.

. The symbol for half-life is t12. Half-life allows the calculation of the time required for plasma concentrations to reach steady-state after starting or changing a dosing regimen. N0 is the initial quantity of the substance that will decay this quantity may be measured in grams moles number of atoms etc Nt is the quantity that still remains and has not yet decayed after a time t.
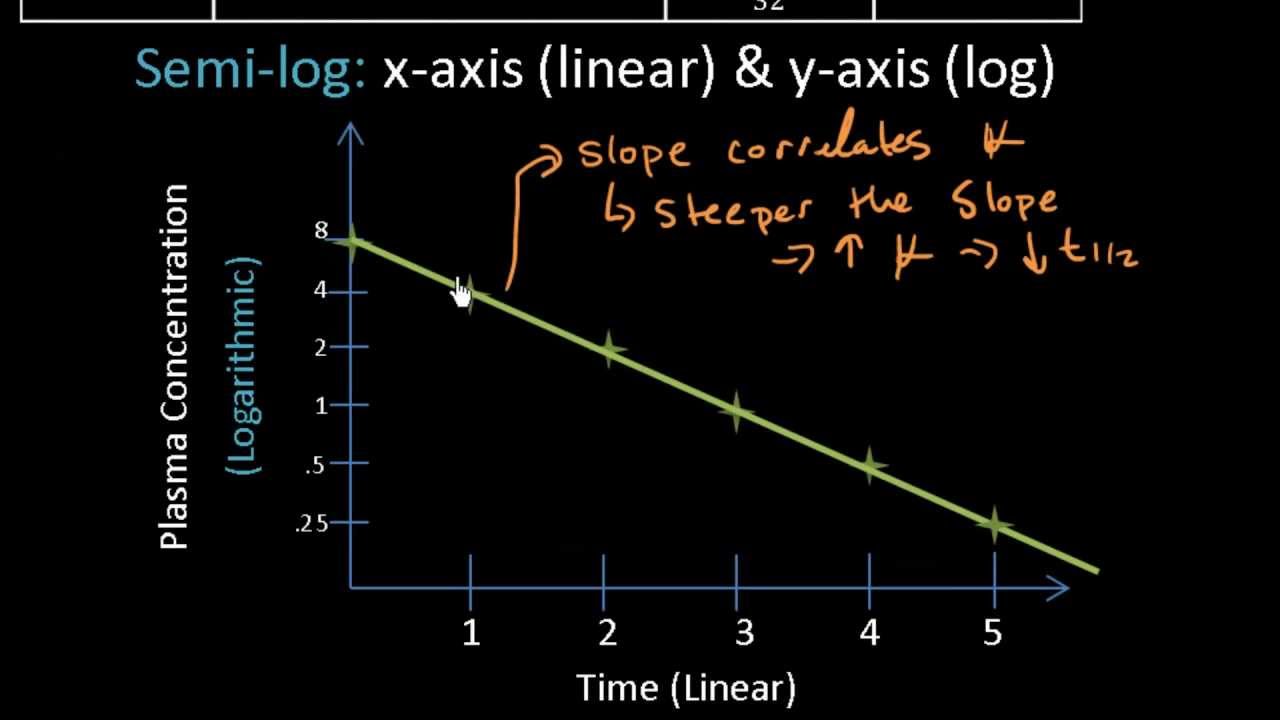
After 4 5 half-lives we are essentially at steady state concentration. The amount of time it takes for the concentration of that medication in the patients blood to be reduced by one half. The half-life for this process is 39 Alternatively half-life is given by where λz is the slope of the terminal phase of the timeconcentration curve for the substance on a semilogarithmic scale.
The half-life can be computed simply by dividing the slope of the curve into 0301 the difference between the logarithm of a number C and the logarithm of number half as large C2. Heres the formula for half-life. Half-life t Vd CL k kee 12 0693 2 0693 ln.
Affiliation 1 Wyeth. Next assume that we stop the infusion. Pharmacology math tutorial for quick exam review.
The formula for half-life is t½ 0693 Vd CL Volume of distribution Vd and clearance CL are required to calculate this variable. Demarcate this time point. T12 0693 Volume of DistributionClearance As demonstrated by the formula a drugs half-life is directly dependent on its volume of distribution or how widely the drug spreads throughout the body.
Effective half-life in clinical pharmacology J Clin Pharmacol. Half of the amount of time it takes for the concentration of. In such conditions the observed half-life is called apparent half-life.
Intravenous bolus Initial concentration C D 0 Vd Plasma concentration single dose CCe kte 0 ae Plasma concentration multiple dose C Ce e kt k e e 0 1 Peak multiple dose C C e ke max 0 1 Trough multiple dose C Ce e k min ke 0. Describe formulas conversions and other math calculations in pharmacology Provide a description of half-life in pharmacology Define the margin of safety in pharmacology. An exponential decay can be described by any of the following four equivalent formulas.
In other words the more widely the drug distributes in your body the longer it half-life. For drugs with first order kinetics this is a constant. The half-life of a pharmaceutical refers to the amount of time it takes for the concentration of that substance in the body to be reduced by one half.
After 2 half-lives 75 of the drug is gone. Authors H Boxenbaum 1 M Battle. Effective half-life in clinical pharmacology.
Assessment t1 2 ln2 λ ln2 V d C L 0693 V d C L t 1 2 l n 2 λ l n 2 V d C L 0693 V d C L Vd volume of distribution CL clearance λ elimination rate constant CLVd. Half- life t 12 1. 0693 is the logarithm of 2 and represents the exponential rate of elimination assuming elimination is by first order kinetics.
By definition t 12 is the time required for the concentration to fall by one half. 40 41 Half-life is determined by clearance CL and volume of distribution V D and the relationship is described by the following equation. Ad Browse Discover Thousands of Medical Book Titles for Less.
Effective half-life in clinical pharmacology.

First Order Elimination Rate Constant And Half Life A Closer Look Lect 11 Youtube
Loading Dose Pharmacology Flashcards Draw It To Know It

Elimination Rate Constant An Overview Sciencedirect Topics

Pharmacokinetics Mnemonics Epomedicine

Drug Half Life Explained Calculator Variables Examples
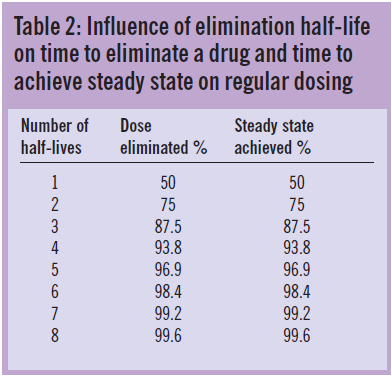
Back To Basics Pharmacokinetics The Pharmaceutical Journal
Half Life Pharmacology Flashcards Draw It To Know It
Back To Basics Pharmacokinetics The Pharmaceutical Journal

Half Life Drug Calculations Practice Problems Part 6 Youtube